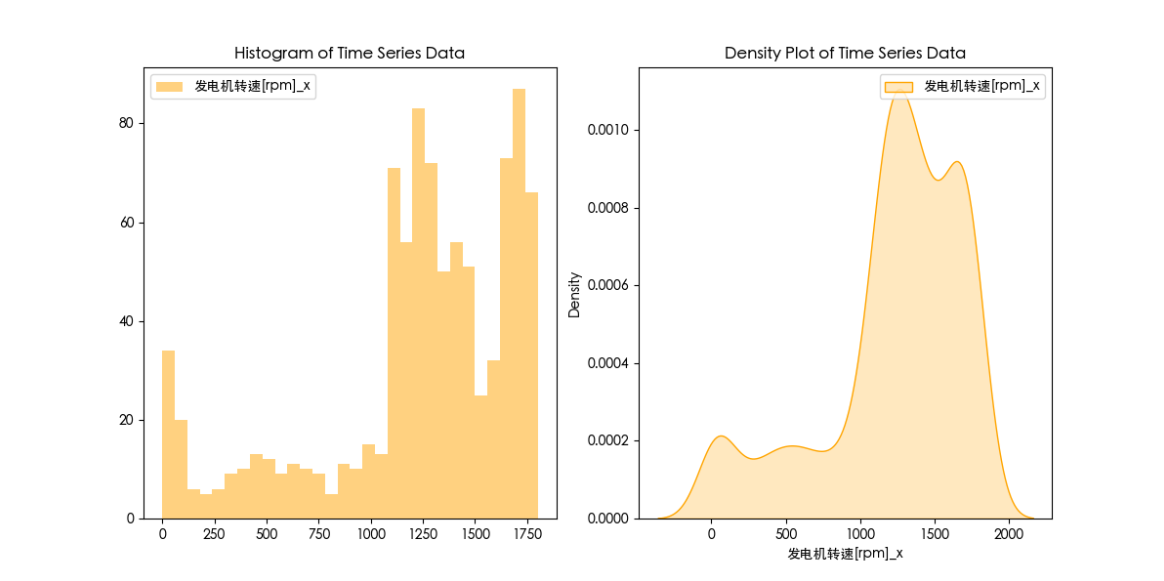
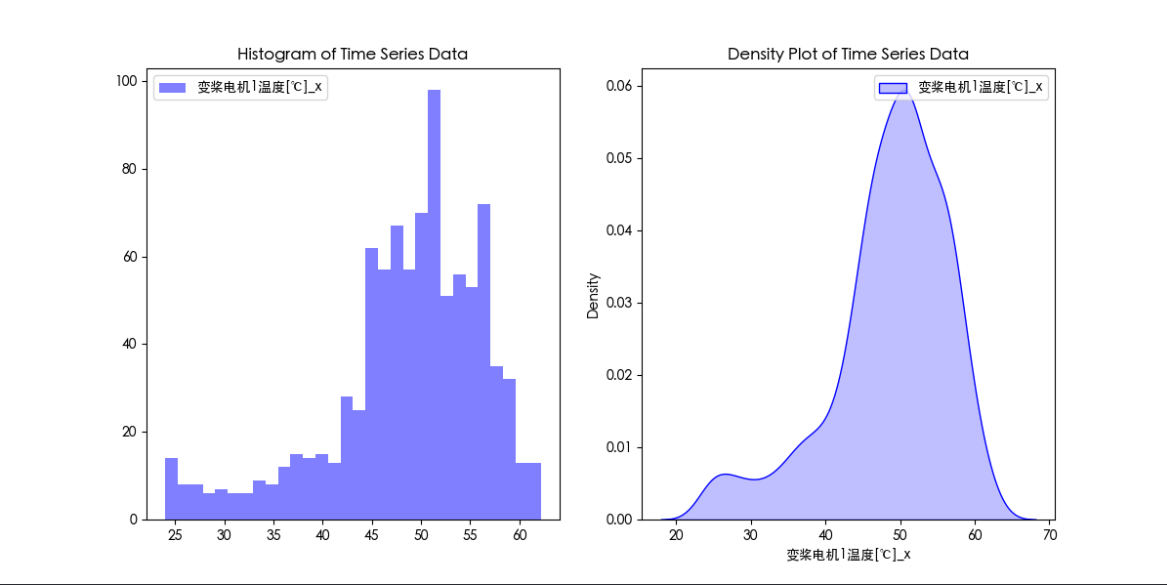
独立同分布

“独立同分布”（Independent and Identically Distributed， i.i.d.），用于描述随机变量的性质：

1. 独立性（Independent）： 如果一组随机变量是独立的，意味着其中一个变量的取值不会提供有关其他变量取值的任何信息。换句话说，一个变量的取值不会影响另一个变量的分布。数学上，对于两个随机变量 X 和 Y，如果它们的联合概率分布等于它们各自的概率分布的乘积，即 P(X, Y) = P(X) * P(Y)，则称它们是独立的。
2. 同分布性（Identically Distributed）： 如果一组随机变量是同分布的，意味着它们具有相同的概率分布。虽然它们可能是独立的，但同分布性强调它们的分布函数相同。数学上，对于一组随机变量 X1, X2, …, Xn，如果它们具有相同的概率密度函数（或概率质量函数），即 P(X1 = x) = P(X2 = x) = … = P(Xn = x)，则称它们是同分布的。

同分布检验代码

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
 
# df = pd.read_csv('your_data.csv')
 
# 选择要比较的两列数据
column1 = 'column_name1'
column2 = 'column_name2'
 
# 创建直方图
plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.hist(df[column1], bins=30, alpha=0.5, color='blue', label=column1)
plt.hist(df[column2], bins=30, alpha=0.5, color='orange', label=column2)
plt.legend()
plt.title('Histogram of Time Series Data')
 
# 创建密度图
plt.subplot(1, 2, 2)
sns.kdeplot(df[column1], shade=True, color='blue', label=column1)
sns.kdeplot(df[column2], shade=True, color='orange', label=column2)
plt.legend()
plt.title('Density Plot of Time Series Data')
 
plt.show()