梯度下降

梯度下降在深度学习领域，它几乎是所有模型训练的基石。尽管它的思想已经深入人心，但我偶尔还是喜欢回到原点，用最简单的例子把这些基础概念重新审视一遍。

我们从一个最纯粹的问题开始：在二维平面上散布着一些数据点 $(x_i,y_i)$，我想用一条直线去拟合它们。

模型与目标

最简单的直线模型，形式如下：

$$\hat{y}=\omega x+b$$

这里的 $\omega$ 和 $b$ 就是我们要通过学习来确定的参数。对于一个给定的真实数据点 $(x,y)$，模型会给出一个预测值 $\hat{y}$。为了衡量预测得好不好，我们需要一个损失函数（Loss Function）。一个最自然、也最常用的选择就是均方误差，这里为了让推导过程尽可能地简洁，我们先只考察单个样本点带来的损失：

$$L=(y-\hat{y}{)}^2=(y-(\omega x+b){)}^2$$

这个式子的含义非常直观：预测值 $\hat{y}$ 与真实值 $y$ 的差距越小，损失 $L$ 就越小，也就意味着我们的直线拟合得越好。我们的最终目标，便是找到一组参数 $(\omega ,b)$，使得在整个数据集上的总损失最小。

梯度计算

梯度下降的核心在于“下降”二字，而“梯度”则为我们指明了方向。为了让损失 $L$ 下降，我需要知道参数该朝着哪个方向调整。这在数学上，就是计算损失函数 $L$ 关于两个参数 $\omega$ 和 $b$ 的偏导数。这只是一个简单的复合函数求导，根据链式法则，整个过程并不复杂。

首先，我们来计算损失 $L$ 对权重 $\omega$ 的偏导数：

$$\frac{\partial L}{\partial \omega }=\frac{\partial }{\partial \omega }(y-(\omega x+b){)}^2=2(y-(\omega x+b))\cdot (-x)=-2(y-\hat{y})x$$

接着，是损失对偏置 $b$ 的偏导数：

$$\frac{\partial L}{\partial b}=\frac{\partial }{\partial b}(y-(\omega x+b){)}^2=2(y-(\omega x+b))\cdot (-1)=-2(y-\hat{y})$$

这样一来，我就得到了损失函数 $L$ 在参数空间 $(\omega ,b)$ 中的梯度向量 $\nabla L$：

$$\nabla L=\left(\frac{\partial L}{\partial \omega },\frac{\partial L}{\partial b}\right)=\left(-2(y-\hat{y})x,-2(y-\hat{y})\right)$$

在数学上，梯度向量指向的是函数值上升最快的方向。而我们的目标是让损失减小，所以很自然地，我们应该沿着梯度的反方向去更新参数。

“下山”的直觉

我喜欢把这个优化过程想象成一个三维的场景。我们可以把参数 $\omega$ 和 $b$ 看作是一个二维平面上的两个坐标轴，而损失函数 $L(\omega ,b)$ 的值则是这个平面上方的高度。这样就构成了一个三维的、通常是碗状的曲面。 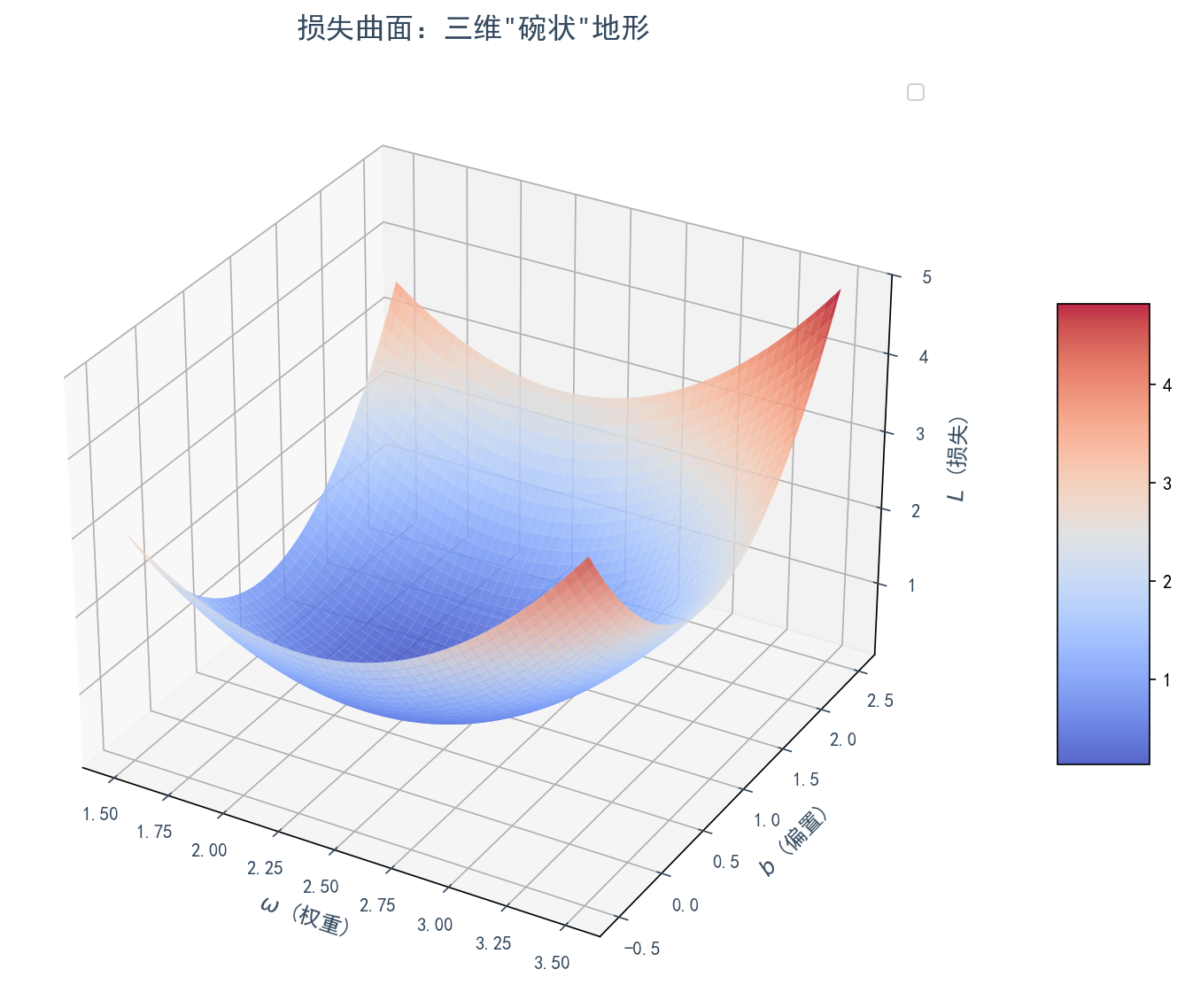我们的任务，就像是站在这个曲面的某个随机的山坡上，想要走到山谷的最低点。梯度 $\nabla L$指向的是上山最陡峭的方向。那么，要下山，我只需要朝着它的反方向 $-\nabla L$ 迈出一步即可。

假设我设定一个步长，在机器学习中我们称之为学习率（Learning Rate），记作 $\eta$。那么每一步的参数更新规则就可以写出来了：

$${\omega }_{\text{new}}\leftarrow {\omega }_{\text{old}}-\eta \cdot \frac{\partial L}{\partial \omega }={\omega }_{\text{old}}+2\eta (y-\hat{y})x$$ $$b_{\text{new}}\leftarrow b_{\text{old}}-\eta \cdot \frac{\partial L}{\partial b}=b_{\text{old}}+2\eta (y-\hat{y})$$

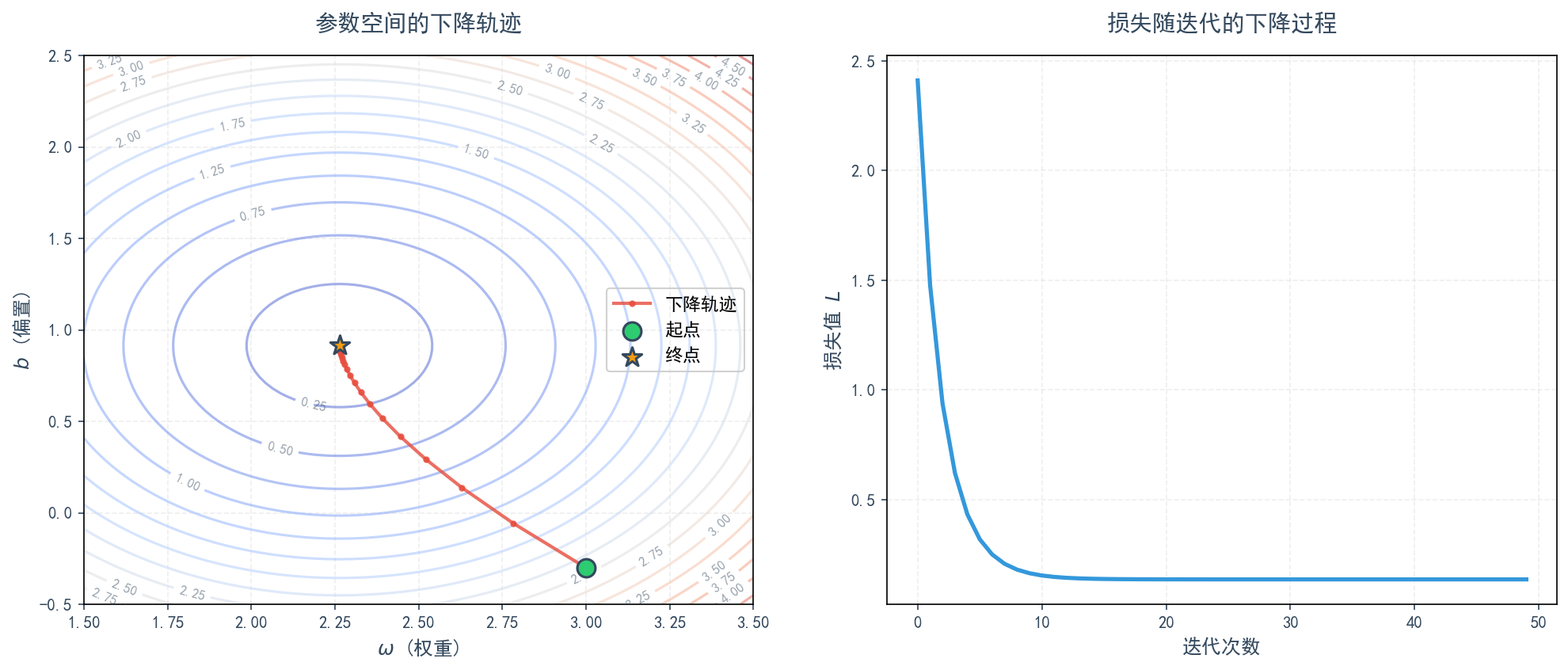
这里值得注意的是，我们上述的梯度计算，仅仅是基于一个随机抽取的样本点 $(x,y)$ 得出的。每拿到一个样本，就计算一次梯度并更新一次参数，这个过程就是随机梯度下降（Stochastic Gradient Descent, SGD）。从随机近似（Stochastic Approximation）的理论来看，尽管每一步的更新方向都带有一定的随机性和“噪声”，但只要学习率 $\eta$ 设置得当，这一系列看似杂乱的步伐，总体上是朝着让总损失减小的方向前进的，最终能够引导我们走到那个理想的“谷底”附近。 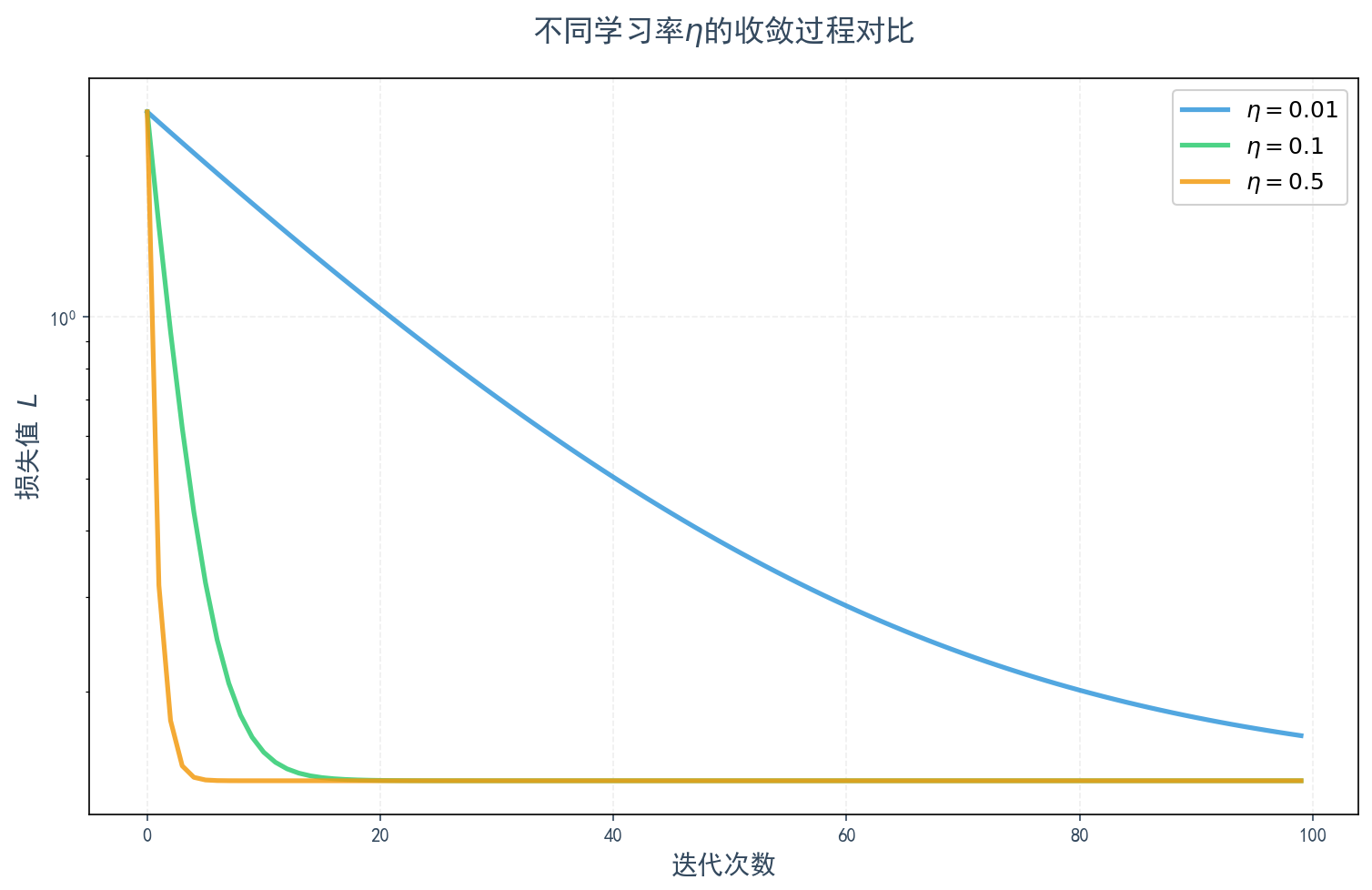从这个最简单的例子中，我们能清晰地看到梯度下降的本质：通过计算梯度来寻找下降方向，并以小步迭代的方式逐步逼近最优解。无论是多么复杂的神经网络，其训练的核心思想，也无外乎是这个朴素过程的延伸和拓展。

x的角色

写到这里，我突然冒出一个问题。在那个 $(\omega ,b,L)$ 的三维空间里，我们一直在讨论参数 $\omega$ 和 $b$ 这两个坐标轴，以及损失 $L$ 这个高度。那么，我们的数据 $x$ 到底扮演了什么角色？它也是一个坐标轴吗？

仔细一想，并非如此。$x$（以及它的搭档 $y$）并不是这个空间的坐标，相反，它们是这个空间“地形”的塑造者。

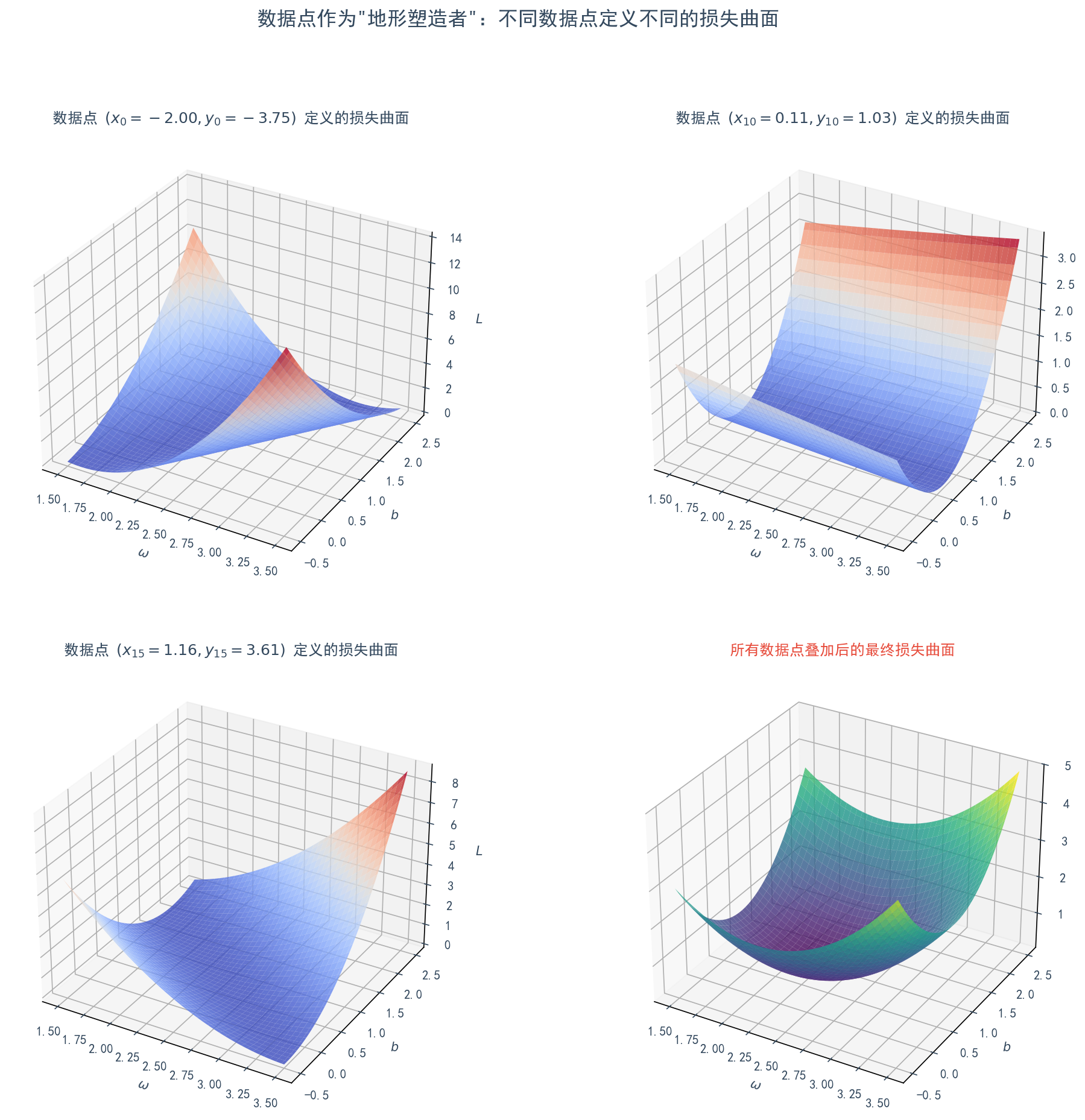
我们可以这样来理解：

1. 单个数据点的作用：假设我们的数据集只有一个点 $(x_i,y_i)$。这个点本身就定义了一个完整的三维“碗状”曲面。你任意选定一组 $(\omega ,b)$，就可以根据公式 $L=(y_i-(\omega x_i+b){)}^2$ 计算出唯一的损失值 $L$。在这个计算中，$x_i$ 和 $y_i$ 是固定的常数，所以它们共同决定了这个“碗”的形状、位置和最低点。

2. 不同数据点，不同地形：现在，我们换一个数据点 $(x_j,y_j)$。它会定义出另一个不同的“碗”。也许这个碗更陡峭，或者碗底在 $(\omega ,b)$ 平面上的位置不同。

3. 整个数据集的作用：我们整个训练任务所面对的最终损失曲面，实际上是数据集中所有点所定义的“碗”的叠加或平均。每一个数据点 $(x_i,y_i)$ 都贡献了它自己的地形特征，所有这些特征融合在一起，形成了我们最终需要下降的那个复杂而唯一的山谷。

这个想法可以从我们刚刚推导的梯度公式中得到印证： $\frac{\partial L}{\partial \omega }=-2(y-\hat{y})x$。

$x$ 直接出现在了 $\omega$ 的梯度公式里。这意味着：

• x 决定了在 w 方向上的坡度：当一个数据点的 $|x|$ 很大时，它计算出的 $\frac{\partial L}{\partial \omega }$ 也会相应变大（在误差项不为零的情况下）。这意味着这个数据点对 $\omega$ 的更新会施加更大的“拉力”，它在塑造损失曲面时的话语权更重，使得在那个点的局部地形在 $\omega$ 方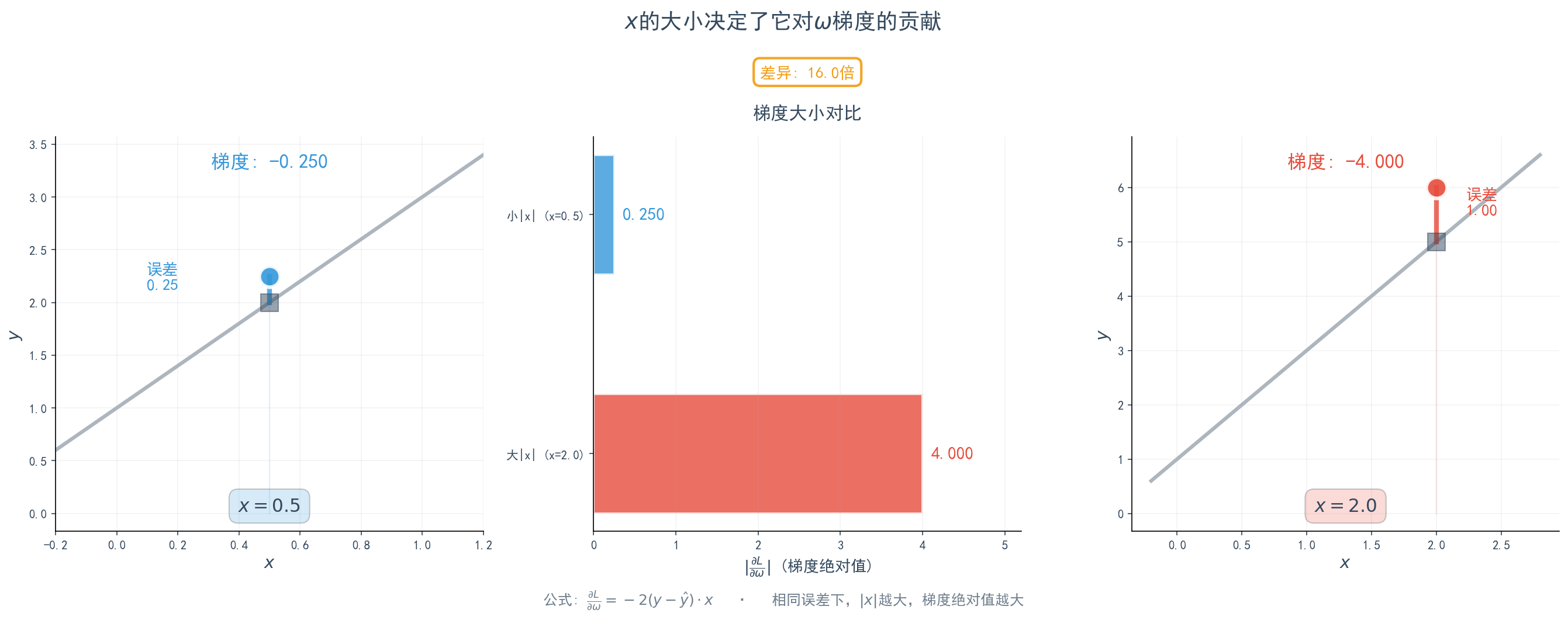向上更“陡峭”。
• 如果某个数据点的 $x=0$，那么它对 $\omega$ 的梯度就为 0。这意味着这个点完全无法告诉我们应该如何调整斜率 $\omega$。这跟我们的直觉是相符的——一个在y轴上的点，无论直线斜率怎么变，只要截距 $b$ 合适，直线都能穿过它。

所以，在 $(\omega ,b,L)$ 的三维空间中，$x$ 不是一个维度，而是定义这个空间“地形”的关键常数。数据集里的每一个 $x$（和 $y$）都像一个引力源，共同塑造了最终的损失曲面，而梯度下降算法就是在这个被 $x$ 和 $y$ 塑造好的地形上寻找最低点的过程。

再进一步：关于“噪声”的思考

我们刚才提到，最终的损失曲面是所有数据点定义的“碗”的叠加或平均。这里就引出了一个更深刻的问题：我们为什么要进行叠加或平均？如果每个数据点 $(x_i,y_i)$ 都代表了一个“真相”，那它们定义的地形为什么会不一样呢？这背后其实就牵涉到我们如何看待“噪声”。

在建模的语境下，“噪声”通常指数据中不能被你当前选定模型所解释的部分。它可能来源于测量误差，也可能源于系统内在的随机性，或者——这是最关键的一点——来源于模型本身的局限性。当你试图用一个简单的线性模型 y = wx + b 去拟合一个本质上更复杂的现实关系时，那些模型无法捕捉到的真实结构，在模型看来，就表现为了“噪声”或“误差”。

我们之所以要对所有数据点的损失进行平均，正是为了找到一个能在所有这些带有“噪声”的、不完全一致的“地形”之间取得最佳平衡的模型。我们希望模型能学习到数据背后那个普遍的、可泛化的“信号”，而不是被单个数据点独特的“噪声”所绑架。后者正是我们常说的“过拟合”。

这个问题再往下想，就触及了建模的哲学边界。我们观察到的数据，究竟是一个确定性世界因为我们信息不完备而产生的“表观随机”，还是说，“可能性”和“随机性”本身就是世界的底层逻辑？

这背后是两种世界观的碰撞：

1. 经典决定论（拉普拉斯妖）：这个观点认为，现实世界在根本上是确定性的。每一个事件都由其之前的原因严格决定。我们之所以需要“概率”和“噪声”，完全是因为我们信息不完备。所谓的“噪声”，本质上都是未被我们建模的、更精细的“信号”。如果有一个“拉普拉斯妖”能知道宇宙中所有粒子的状态和所有作用力，那么一切都是可以被完美预测的，“噪声”将不复存在。

2. 内禀随机性（量子力学）：这个观点则认为，宇宙的底层逻辑是概率性的。比如，一个放射性原子何时衰变是内禀随机的，我们无法用任何“隐藏变量”来精确预测，只能给出一个概率。在这个世界观里，即使是“拉普拉斯妖”，也无法精确预测一切。噪声中，至少有一部分是不可约减的、源于世界本源的随机性。

作为一个从事算法工作的人，我的感受是，在实践层面，我们通常采取一种实用的决定论立场。我们假定我们处理的宏观系统在很大程度上是因果决定的，我们的任务就是尽可能地用更强大的模型、更丰富的数据去逼近这个因果关系，将更多的“噪声”转化为可解释的“信号”。

但同时我们也要保持谦卑，承认我们的模型永远只是对现实的一种抽象和简化，并且宇宙的本源可能就存在着不可预测的随机性。一个好的模型，其价值不在于成为现实本身，而在于它强大的解释和预测能力，它恰恰懂得应该“忽略”掉哪些信息。