LearningRate和BatchSize

Batch Size 和 Learning Rate 的缩放

看了苏剑林老师的 当Batch Size增大时，学习率该如何随之变化？，做一个简单记录。

一个几乎每个做深度学习的朋友都会遇到的困惑：当我的计算资源增加了，比如从一块 GPU 换到了四块，很自然地，我会想通过增大 Batch Size 来加速训练。但紧接着的问题就是，Learning Rate应该如何随之调整？

最理想的情况，我们当然是希望算力翻倍，时间减半，这是一种朴素的线性思维。但稍有实践经验的朋友都知道，事情远没有这么简单。如果你只是单纯地增大 Batch Size 而不做任何其他调整，模型的性能很可能急剧下降，甚至完全无法收敛。在众多超参数中，学习率是那个最需要与 Batch Size 联动调整的关键变量。

这篇文章，我想和大家一起梳理一下关于 Batch Size ($B$) 和学习率 ($\eta$) 之间的“缩放定律”（Scaling Law）的思考。本质上，我们是在探寻一个根本问题：当 $B$ 变大 $k$ 倍时，$\eta$ 应该如何变化，才能让我们的训练既高效又稳定？

回到起点：从“梯度方差”的视角看

要理解这个问题，我们不妨先回到最初的起点，看看早期大家是如何从“梯度噪声”这个角度来理解它的。这是一种非常直观的思路。

我们在训练中用一个 Mini-Batch 计算出的梯度，只是对“真实梯度”（用全部数据算出的梯度）的一次带噪估计。当增大 Batch Size，就相当于在更多的样本上进行了平均，得到的梯度估计就更准确，其方差（或说噪声）就更小。既然梯度的方向更加可靠了，我们自然就可以沿着这个方向迈出更大的一步，也就是增大学习率。

历史上，有两个经典的“经验法则”。

1. 二次方根缩放 ($\eta \propto \sqrt{k}$)

它背后的数学思想是，在随机梯度下降（SGD）的过程中，我们希望每一步更新引入的噪声强度保持不变。数学上可以推导，如果你将 Batch Size 扩大到 $k$ 倍，梯度的噪声标准差会减小到原来的 $1/\sqrt{k}$ 倍。为了抵消这种减小，让总的更新“扰动”水平维持原样，我们就需要把学习率相应地扩大到 $\sqrt{k}$ 倍。

2. 线性缩放 ($\eta \propto k$)

实践中，二次方根缩放这条规则似乎太过“保守”了。在很多场景下，一个更激进、也更广为人知的策略——线性缩放——效果要好得多。它的直觉非常简单：如果我用了一个 $k$ 倍大的批次，就相当于一次性处理了过去 $k$ 个小批次的数据。为了在一步之内达到过去 $k$ 步的效果，最直接的想法就是把步长（学习率）也乘以 $k$。

一个更本质的视角：直面“损失函数”

但是，这种基于“梯度噪声”的分析有一个绕不过去的坎：它们都隐隐暗示着，只要我的 Batch Size 足够大，学习率就可以无限地增长下去。这显然与我们的实践经验相悖——任何模型的学习率都有一个上限，超过它，训练过程就会因振荡而发散。

苏老师提到了一篇openai的文章: An Empirical Model of Large-Batch Training

这里面的推导略微复杂，涉及到了对损失函数的二阶泰勒展开，但它的最终结论却异常漂亮和深刻。我们先不急着陷入数学细节，直接来看这个针对 SGD 优化器的关键公式：

${\eta }_{opt}(B)=\frac{{\eta }_{max}}{1+{\mathcal{B}}_{noise}/B}$

我们来一起拆解一下这个公式的各个部分：

• ${\eta }_{opt}(B)$：对于给定的 Batch Size $B$，我们应该使用的最佳学习率。
• $B$：就是我们当前的 Batch Size。
• ${\eta }_{max}$：这是一个极其重要的参数，我称之为“最大学习率上限”。公式告诉我们，无论 $B$ 变得多大，我们的学习率都不应该超过这个“天花板”。
• ${\mathcal{B}}_{noise}$：这是另一个关键参数，可以理解为一个“临界批大小”或者“特征批大小”，它标志着两种不同训练状态的边界。

简单绘制图像可以清晰的看到学习率随 $B$ 变化的趋势：

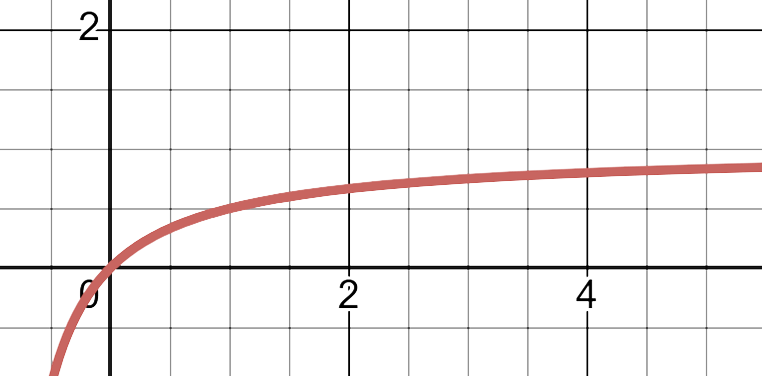
这个公式统一了我们之前的观察：

1. 当 Batch Size 很小 ($B\ll {\mathcal{B}}_{noise}$) 时：此时分母中的 ${\mathcal{B}}_{noise}/B$ 远大于 1，所以 1 可以忽略，公式近似为 ${\eta }_{opt}(B)\approx \frac{{\eta }_{max}}{{\mathcal{B}}_{noise}/B}=(\frac{{\eta }_{max}}{{\mathcal{B}}_{noise}})\cdot B$。我们看到，${\eta }_{opt}$ 和 $B$ 呈现出纯粹的线性关系。这说明，在小批次训练阶段，“批大小加倍，学习率加倍”的线性缩放法则是非常好的近似。

2. 当 Batch Size 很大 ($B\gg {\mathcal{B}}_{noise}$) 时：此时分母中的 ${\mathcal{B}}_{noise}/B$ 趋近于 0，于是 ${\eta }_{opt}(B)\approx {\eta }_{max}$。学习率的增长开始饱和，并逐渐逼近它的理论上限 ${\eta }_{max}$。这时，我们再疯狂地增大 $B$，学习率已经提不上去了，投入更多算力所换来的训练加速效果也就微乎其微了。

这个漂亮的公式给了我们一个非常清晰的实践启示：对于 SGD，“线性缩放”是一个很好的出发点，但它只在 Batch Size 小于某个“临界点” ${\mathcal{B}}_{noise}$ 时才有效。超过这个点再盲目增大批次，就是一种对计算资源的浪费。

Adam 的“涌现现象”

上面的分析都是针对 SGD的。但现在我们最常用的优化器是 Adam 这类自适应优化器。

对 Adam 的分析过程要复杂得多，为了抓住主要矛盾，研究者通常会将其近似为一种更简单的优化器（比如 SignSGD）来进行推导。

对于 SGD，我们看到最佳学习率 ${\eta }_{opt}$ 随着 $B$ 的增大，是单调递增或者趋于平稳的。但对于 Adam，情况并非总是如此。分析表明：

• 对于较小的 Batch Size：Adam 的行为更符合二次方根缩放（$\eta \propto \sqrt{k}$），而不是线性缩放。
• 对于非常大的 Batch Size：可能会出现一个“涌现”——存在一个最佳的批大小 $B_{surge}$，当我们的 Batch Size 超过这个值之后，最佳学习率反而需要减小！

这个现象实在是太奇怪了，它违背了我们“批次越大，步子越稳，学习率应该越大”的朴素认知。我们该如何理解它呢？一个比较好的直观解释是：Adam 本身是一个“聪明”的优化器，它会为每个参数自适应地调整学习的步伐。在 Batch Size 较小时，梯度中包含的噪声在某种程度上是有益的，它像一种正则化，可以防止 Adam “过于自信”地在某个方向上冲得太猛而陷入局部最优。而当 Batch Size 变得极大时，梯度变得极其精确，这种有益的“噪声修正”效应就消失了。为了弥补这一点，我们反而需要变得更加保守，主动降低学习率来保证训练的稳定。

步数 vs. 样本数

将所有这些零散的发现串联起来，我们最终可以得到一个关于训练效率的、相当普适和优美的权衡关系。这个关系把我们从具体的优化器中解放出来，看到了一个更宏观的图景。

这个关系联系了两个我们最关心的指标：

• $S$：训练收敛所需的总步数（iterations）。
• $E$：模型在训练过程中看过的总样本数，也就是 $E=S\times B$。

它们之间存在一个近似的反比关系，我把它写成一个简化的形式：

$(S-S_{min})(E-E_{min})\approx \text{常数}$

这里 $S_{min}$ 和 $E_{min}$ 分别是理论上可能达到的最少步数和最少样本数。

我们不可能同时达到“最少的训练步数”和“最少的样本数”，鱼和熊掌不可兼得。

1. 追求最少的训练步数 (小 $S$)：这意味着你要用非常大的 Batch Size。这在拥有海量 GPU 资源时是“计算高效”的，因为它减少了迭代次数和通信开销。但代价是，你的模型需要看过非常多的总样本量（大 $E$）才能收敛，这是一种“数据上的浪费”。

2. 追求最少的样本数 (小 $E$)：这意味着你应该用非常小的 Batch Size。这被称为“数据高效”，在数据集很宝贵时非常重要。但缺点是，你需要进行极其漫长的训练步数（大 $S$）才能达到同样的效果，这可能会花费很长的时间。

小结

最后，我想把这些思考总结为几点可供大家参考的实践建议：

1. 不要盲目增大 Batch Size：增大它的同时，必须联动地调整学习率。
2. “线性缩放”是很好的起点：当你使用 SGD，并且只是适度地增大 Batch Size（比如 2 倍或 4 倍）时，将学习率也乘以相同的倍数，通常是一个非常有效的初始尝试。
3. 认识收益递减点：对于模型和数据，客观上存在一个“临界批大小” ${\mathcal{B}}_{noise}$。将 Batch Size 设置得远超这个值通常是浪费计算资源，因为你已经无法通过提高学习率来获得同等比例的加速了。
4. 警惕 Adam 在大批次下的反常行为：如果你在使用 Adam，并且尝试非常大的 Batch Size，请务必小心“涌现现象”。当训练开始不稳定时，一个反直觉的解决方案可能不是提高，反而是降低学习率。
5. 理解效率的权衡： Batch Size 的选择，本质上是在“计算效率”（追求更少的迭代步数）和“数据效率”（追求更少的总样本）之间做权衡。这个选择，最终取决于你拥有的计算资源和数据资源。