场景设定:估计一枚硬币的正面朝上概率 θ
假设我们有一枚可能不均匀的硬币,我们想知道它正面朝上的真实概率 θ 是多少。为了搞清楚这个问题,我们进行了一系列抛硬币实验。
频率学派
频率学派认为,概率是事件在大量重复实验中发生的长期频率。对于硬币的例子,θ 是一个未知但固定不变的常量。我们无法对 本身进行概率描述(比如“ 有95%的概率在某个区间”是错误的说法),因为一个常量要么是某个值,要么不是,没有概率可言。我们的目标是通过样本数据来估计这个唯一的真值 。
数学方法:最大似然估计 (Maximum Likelihood Estimation, MLE)
这是频率学派最核心的参数估计方法。其思想是:既然我们已经观测到了一系列数据,那么最有说服力的参数 θ 应该是那个最有可能产生这组观测数据的 θ。
我们用代码模拟抛硬币的过程,可以看到随着数据增多,θ 的最大似然估计值变化的情况,并引入频率学派描述不确定性的工具——置信区间 (Confidence Interval)。
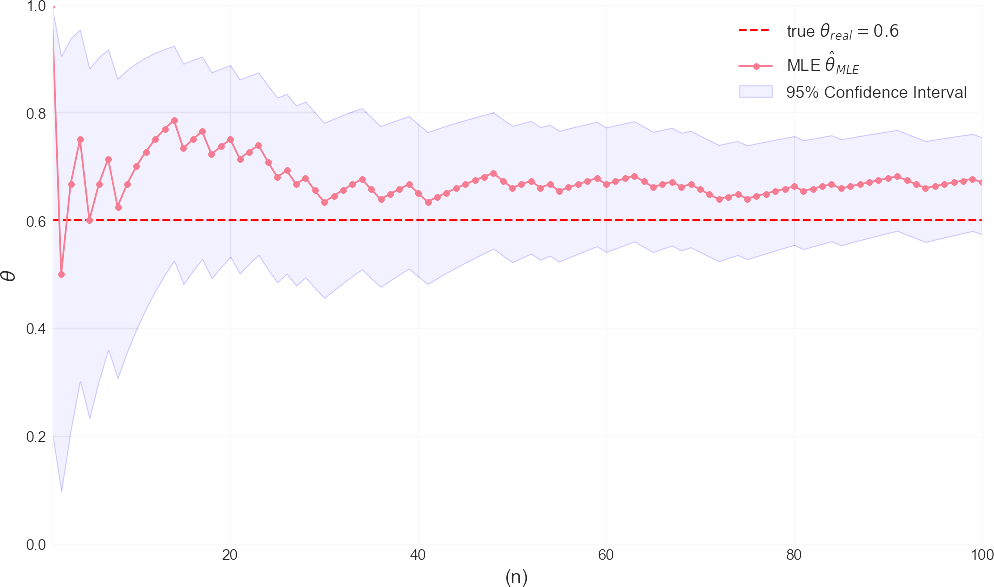
- 浅红色的点线是每次增加观测数据后,计算出的最大似然估计值 。你可以看到它随着数据量的增加,逐渐向红色的真实值 θ∗real 收敛。
- 浅蓝色的区域是95%置信区间。它的正确解释是:如果我们反复进行这整套实验(比如100次抛掷)无穷多次,那么由这些实验所构建出的置信区间中,有95%会包含那个未知但固定的真实参数 θ_real。注意:它并不意味着“真实值有95%的概率落在这个区间内”。这是频率学派和贝叶斯学派最关键的区别之一。
贝叶斯学派
贝叶斯学派认为,概率是对一个命题信任程度的度量 (degree of belief)。因此,我们可以对任何不确定的事物赋予概率,包括参数 θ 本身。在贝叶斯框架下,θ 是一个随机变量,它有一个概率分布。
分析过程是:
- 先验 (Prior):在看到任何数据之前,我们对 θ 有一个初始的信念,这表示为先验概率分布 P(θ)。
- 似然 (Likelihood):和频率学派一样,这是由数据给出的信息 P(data∣θ)。
- 后验 (Posterior):结合先验和似然,我们使用贝叶斯定理来更新我们对 θ 的信念,得到后验概率分布 P(θ∣data)
数学方法:贝叶斯定理
其中:
- 是后验概率:在观测到数据后,我们对 θ 的信念。
- 是似然:与频率学派中的似然函数相同。
- 是先验概率:我们关于 θ 的初始信念。
- 是证据因子或边际似然,它是一个归一化常数,确保后验分布的积分为1。通常可以写成 。
我们使用与上面完全相同的模拟数据,但用贝叶斯方法进行分析。我们会看到,结果不再是一个点估计和一个置信区间,而是一个不断更新的完整概率分布。
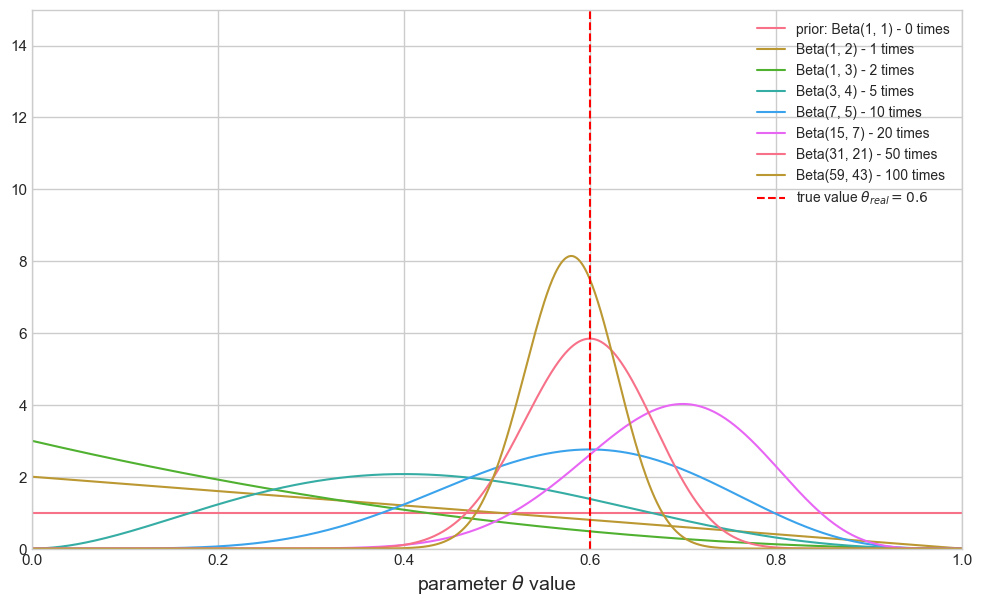
- 最初的虚线(0次抛掷) 是我们的先验分布 ,它是一条平坦的直线(均匀分布),代表我们认为 在
[0, 1]之间取任何值的可能性都一样。 - 随着观测数据一个个进来(1次、2次、…、100次),后验分布曲线不断更新。
- 可以清晰地看到,随着数据量的增加,分布变得越来越窄,并且其峰值越来越接近红色的真实值。
- 这个演变过程完美地体现了贝叶斯思想:通过数据,我们对参数 θ 的不确定性逐渐减小,信念也越来越集中。
- 在100次抛掷后,我们得到的不是一个点,而是一个关于 θ 的完整概率分布。我们可以从中计算出可信区间 (Credible Interval)。例如,一个95%的可信区间是指,我们有95%的把握相信,真实的 值就落在这个区间内。这是一个直接的概率陈述,非常符合直觉
核心区别总结
| 特征 | 频率学派 (Frequentist) | 贝叶斯学派 (Bayesian) |
|---|---|---|
| 概率的定义 | 事件的长期频率 | 对一个命题的信任度 |
| 参数()的本质 | 未知、固定的常量 | 随机变量,有其自身的概率分布 |
| 分析的输入 | 只有数据 | 数据 + 先验知识 (Prior) |
| 分析的输出 | 参数的点估计 (如MLE) 和 置信区间 | 参数的后验概率分布 (Posterior) |
| 不确定性的描述 | 置信区间:描述的是估计方法的长期表现 | 可信区间:直接描述参数本身落在某区间的概率 |
| 核心公式/方法 | 最大似然估计 | 贝叶斯定理 |