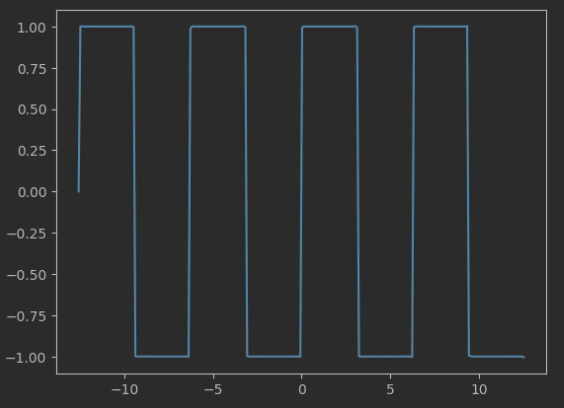
三角函数系的正交性
 这里要证明的话可以用到积化和差公式
这里要证明的话可以用到积化和差公式
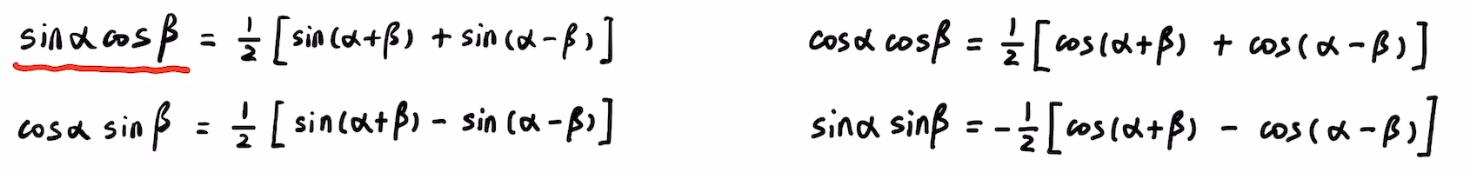
系数推导(对于周期为 的函数)
推导
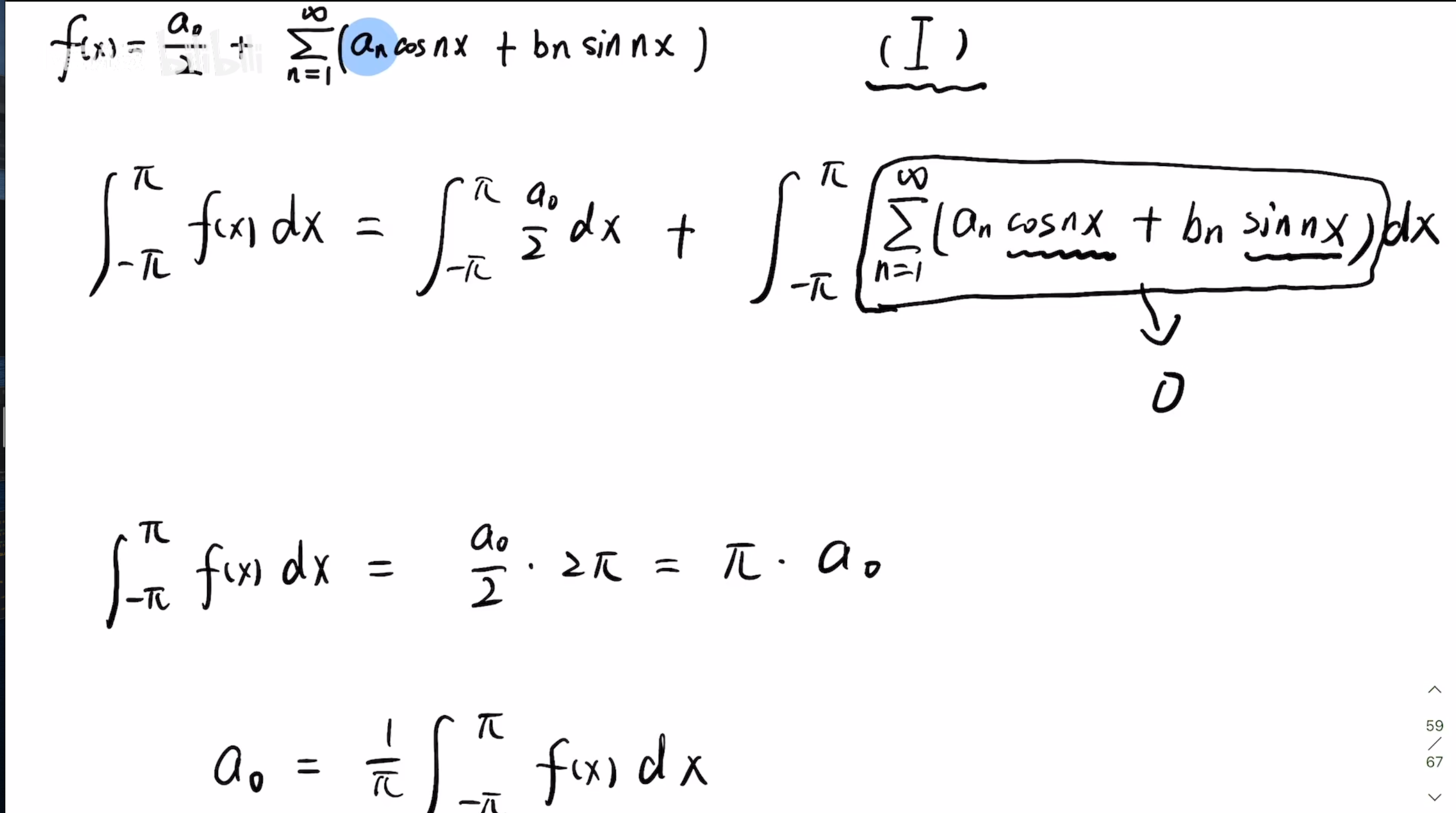
推导
这里给I式两边同乘 ,再到 上积分就会发现I式第二项只剩下了n=k的这一项,然后解出结果能导出
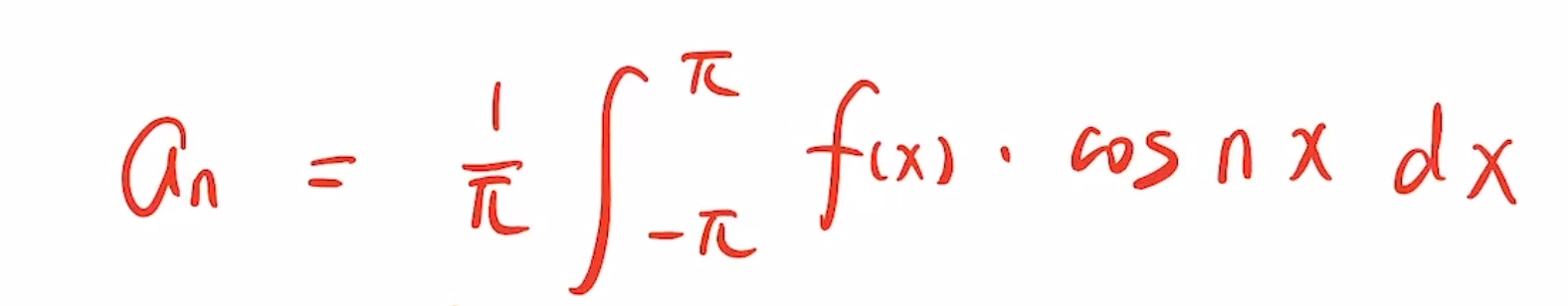
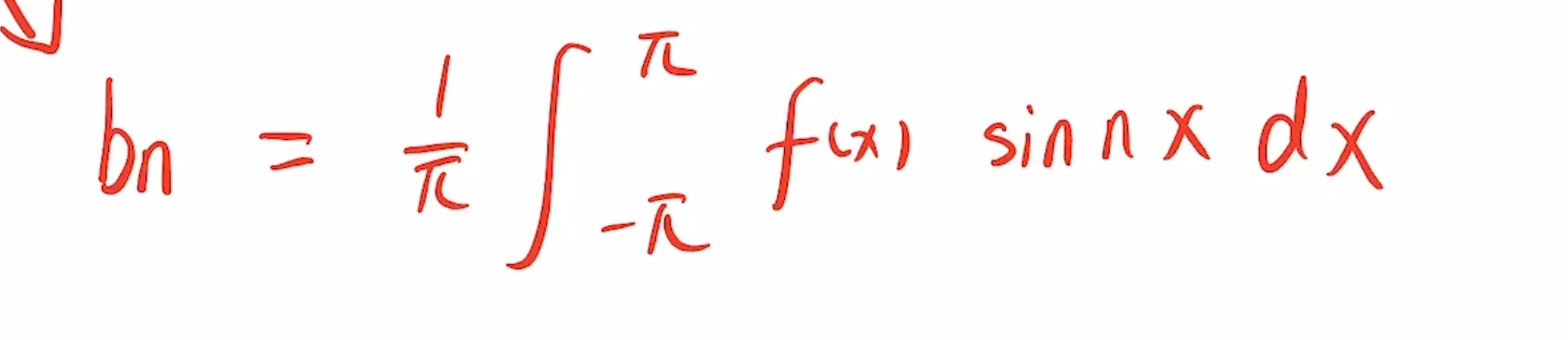
推广
上述公式要推广到任意周期函数,只需要用换元法就可以。
示例
下面的代码用傅里叶级数拟合了一个周期为 6 的方波,可以看到当n为 3000 时,拟合的方波已经非常趋近于真实的方波,肉眼基本上无法分辨。
import numpy as np
t = 4
x = np.arange(-t * np.pi, t * np.pi, 0.1).reshape((-1, 1))
def fourier(ns, x):
n = np.linspace(1, ns, ns).reshape(1, -1)
an = n * 0
bn = 1 / (np.pi * n) * (2 - 2 * np.cos(n * np.pi))
res = an * np.cos(n * x) + bn * np.sin(n * x)
return res.sum(axis=1)
fx = fourier(3000, x)
import matplotlib.pyplot as plt
plt.plot(x, fx)
plt.show()