ARIMA模型的数学公式可以表示为:
ARIMA模型的参数p、d和q需要通过对时间序列数据的分析和模型选择方法(如自相关图ACF、偏自相关图PACF等)进行确定。
需要注意的是,ARIMA模型假设时间序列数据需要具有平稳性,因此在应用ARIMA模型之前,可能需要对非平稳时间序列进行差分处理,以使其成为平稳序列。
参数确定
ARIMA模型有三个参数(p, d, q), p是自回归过程的参数,代表需要考虑多少个历史值作为自回归的输入, d则是建立平稳性过程中差分的阶数, q则是移动平均过程中需要考虑的历史值的数量
p、q: 通过ACF、PACF相关系数进行确定 d: 观察差分序列平稳性
振动数据时间序列预测应用
这里用到的是风机的三天的振动传感器上送的数据,数据特征如下:
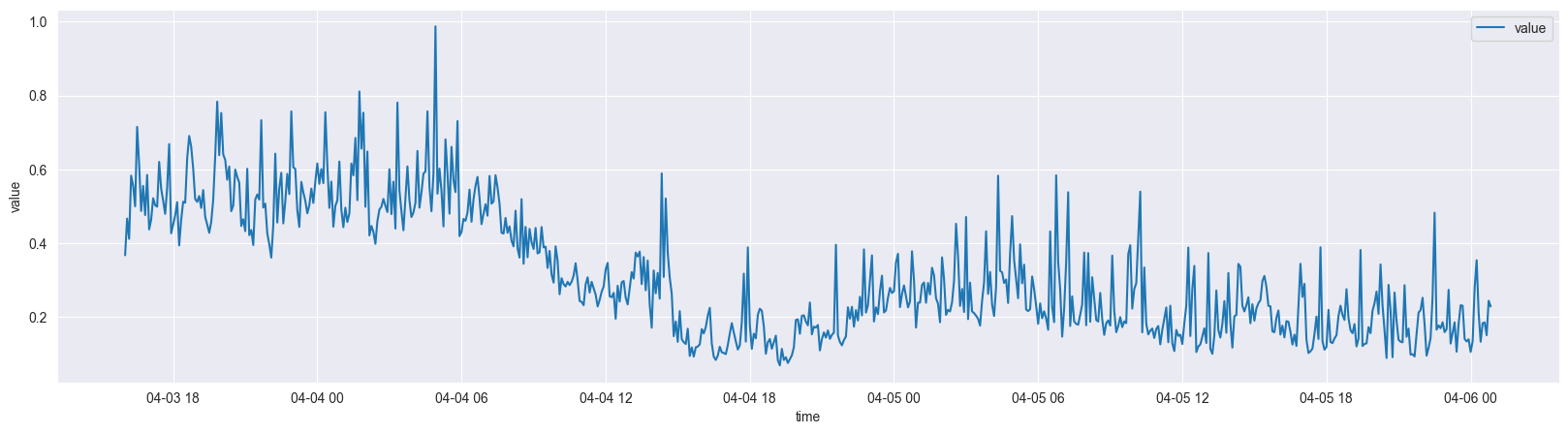
预处理
经过iqr离群值去除后的原始数据、一阶、二阶差分数据, 可以看到一阶差分基本趋于平稳
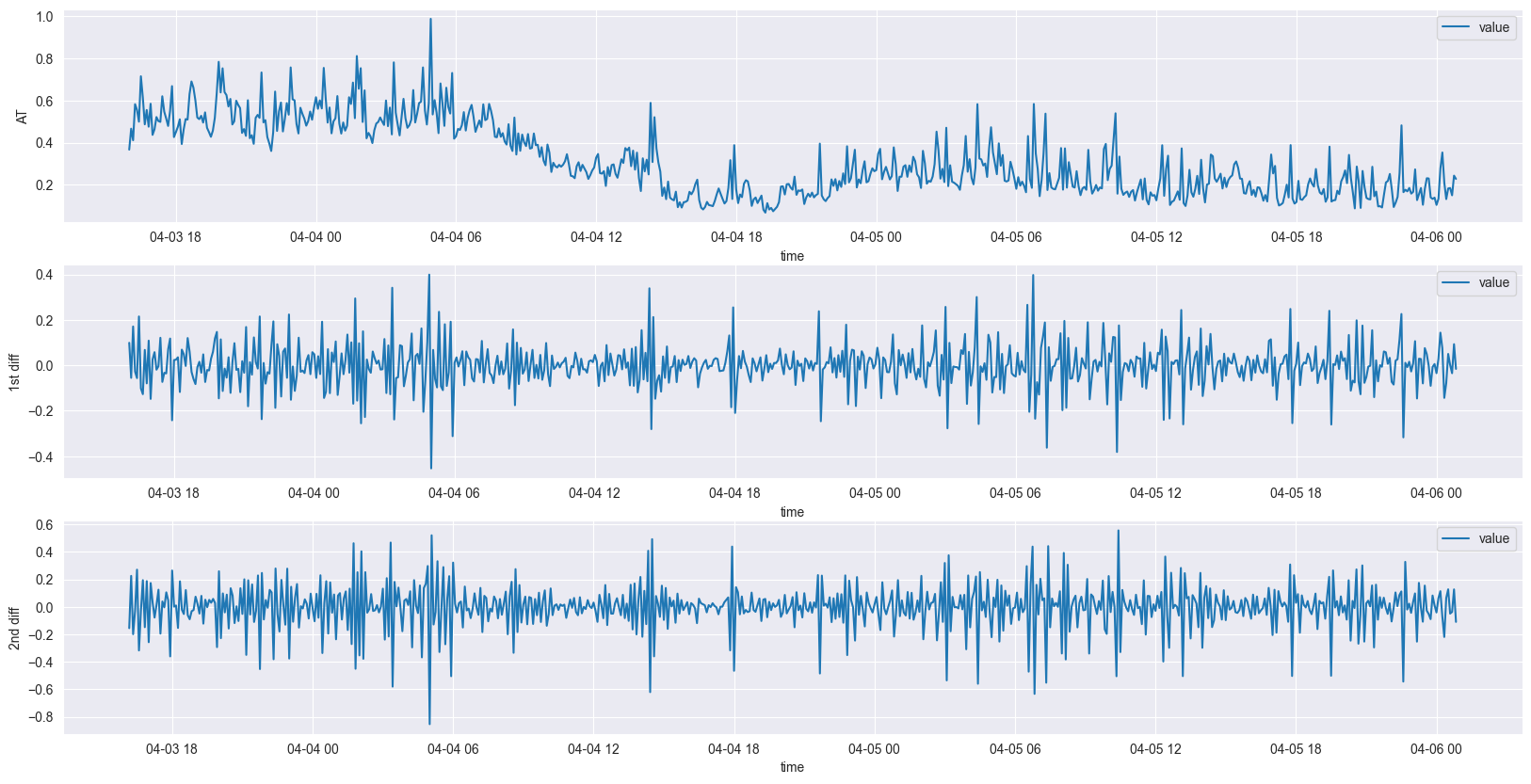
ACF/PACF自相关性判断
fig, axes = plt.subplots(2, 1, figsize=(20, 10))
sm.graphics.tsa.plot_acf(filtered_data, ax=axes[0])
sm.graphics.tsa.plot_pacf(filtered_data, ax=axes[1])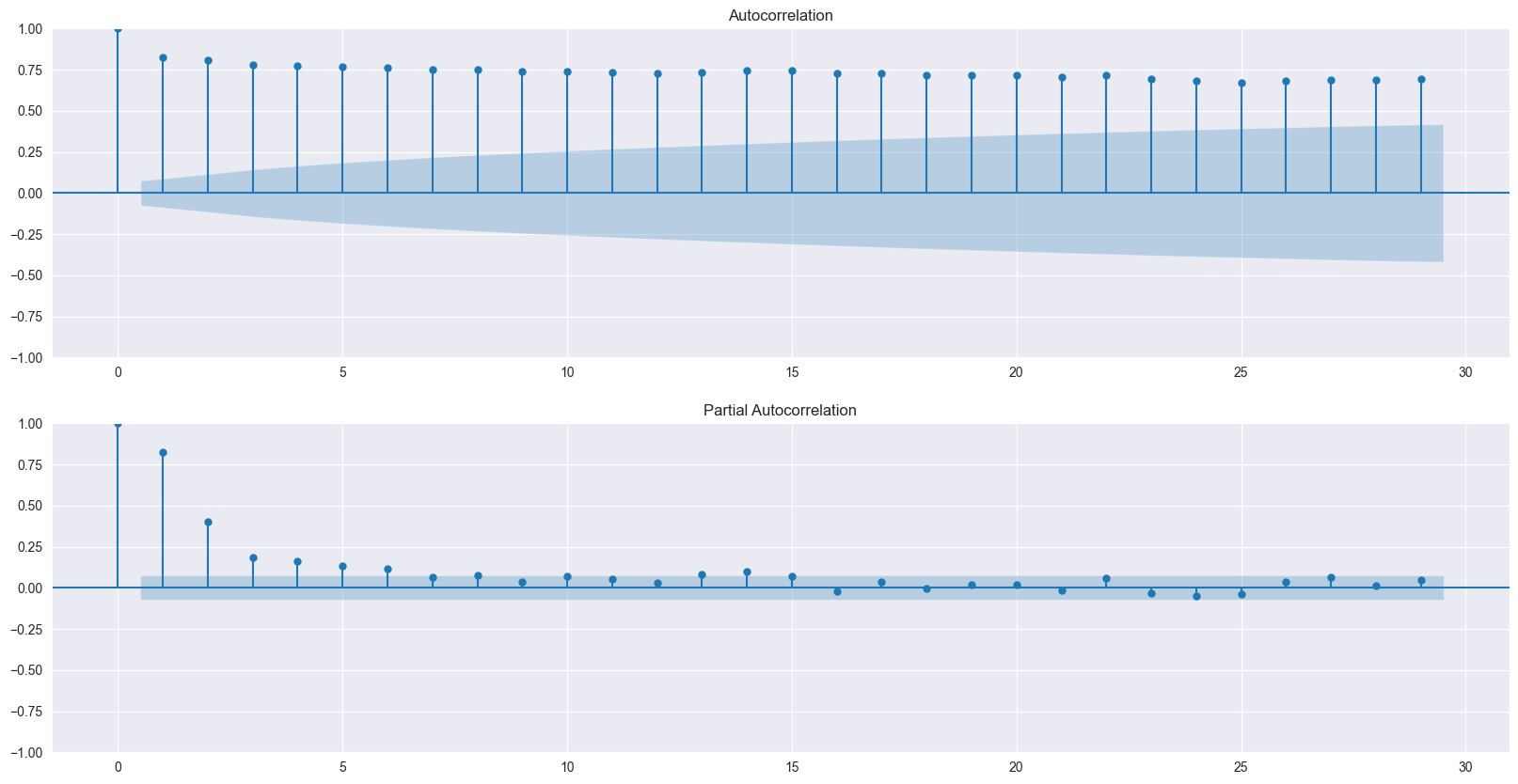
预测结果
p, d, q = 30, 1, 7
model = ARIMA(train, order=(p, d, q))
model_fitted = model.fit()
forcast_data = model_fitted.forecast(100)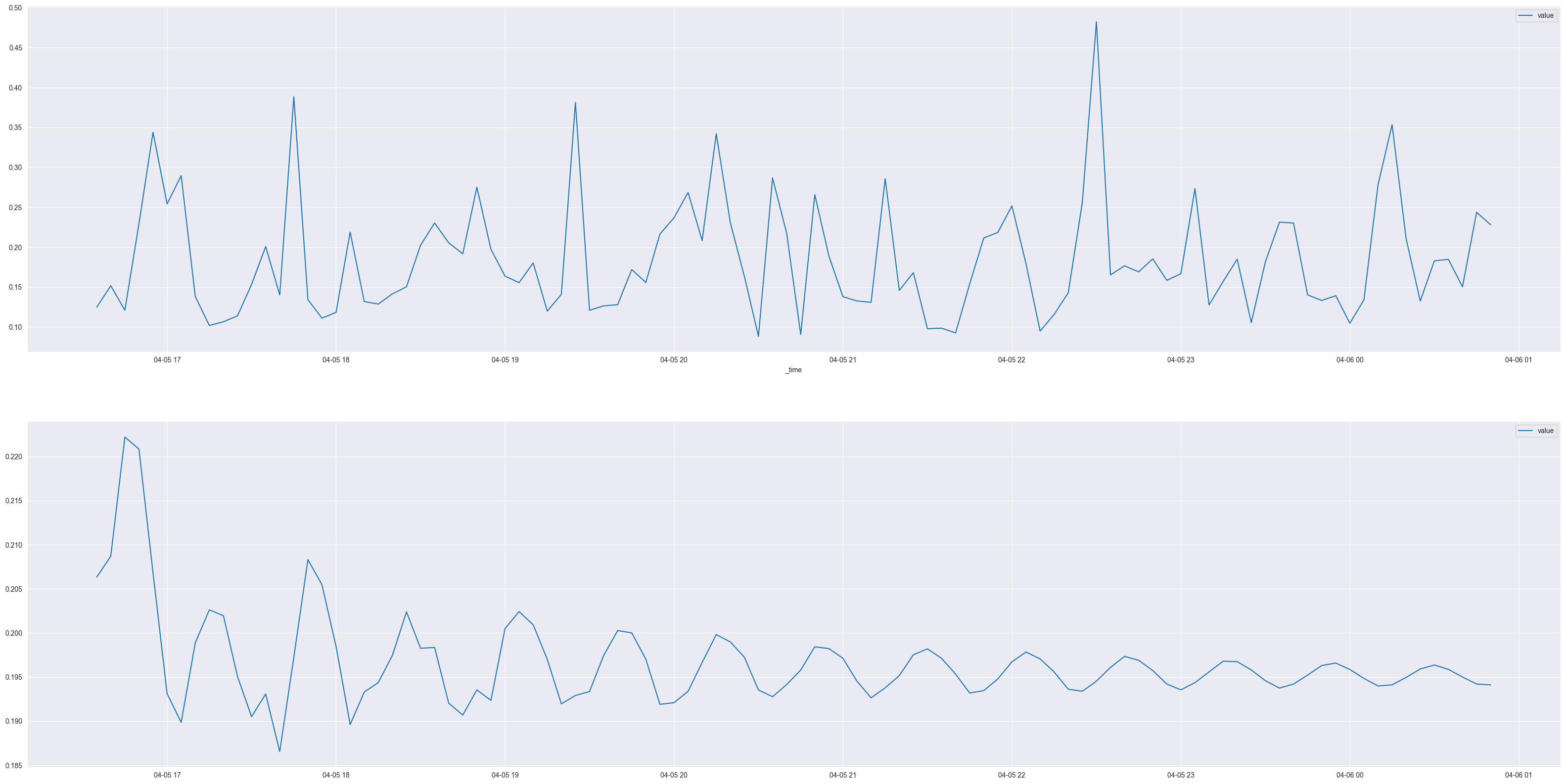
总结
由于时间原因,并没有进行详细的参数搜索,对模型性能的评估也没有完成,但是模型短期内的预测效果是可见的,整体预测数值的趋势较为合理